Fork me on GitHub

『HDU 3068』最长回文

发表于 | 更新于 | 分类于 | 阅读次数：

Problem

Problem Description
给出一个只由小写英文字符a,b,c…y,z组成的字符串S,求S中最长回文串的长度.
回文就是正反读都是一样的字符串,如aba, abba等

Input
输入有多组case,不超过120组,每组输入为一行小写英文字符a,b,c…y,z组成的字符串S
两组case之间由空行隔开(该空行不用处理)
字符串长度len <= 110000

Output
每一行一个整数x,对应一组case,表示该组case的字符串中所包含的最长回文长度.

Sample Input
aaaa
abab

Sample Output
4
3

Solution

这道题是一道Manachar模板题

Manacher

背景

解决的问题就是：
给定一个字符串，求出其最长回文子串。例如：

  • s=”abcd”,最长回文长度为 1；
  • s=”ababa”,最长回文长度为 5；
  • s=”abccb”,最长回文长度为 4，即 bccb。
    以上问题的传统思路大概是，遍历每一个字符，以该字符为中点向两边查找。其时间复杂度为O(n^2)，很不高效，但这个思想我们下面要用到。而在1975年，一个叫Manacher的人发明了一个算法，该算法可以把时间复杂度提升到O(n)。下面来看看该算法是如何工作的。

算法过程

由于回文分为偶回文（比如 bccb）和奇回文（比如 bcacb），而在处理奇偶问题上会比较繁琐，所以这里我们使用一个技巧，在字符间插入一个字符（前提这个字符未出现在串里）。举个例子：s=abbahopxpo转换为s_new=$#a#b#b#a#h#o#p#x#p#o#（这里的字符 $; 只是为了防止越界，下面代码会有说明），如此，字符串s里起初有一个偶回文abba和一个奇回文opxpo，被转换为#a#b#b#a#和-#o#p#x#p#o#，长度都转换成了奇数。

定义一个辅助数组p，p[i]表示以snew[i]为中心的最长回文的半径，例如：

可以看出，p[i]-1正好是原字符串中最长回文串的长度。
Manacher算法之所以快，就快在对 p 数组的求法上有个捷径。在我们解决了奇偶回文的繁琐时，剩下的难点就是求 p 数组，按照普通思维，我们是这样求解的：求解p[i]，先初始化p[i]=1，再以snew[i]为中心判断两边是否相等，相等就将p[i]+1。这就是之前我们提到的传统思路，但是我们想想，能否让p[i]的初始化不是 1，让它更大点，看下图：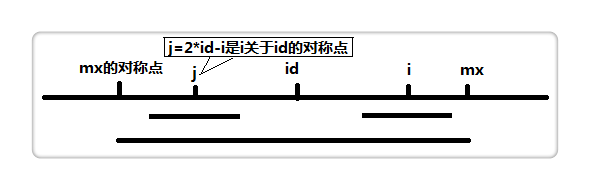

于是我们可以这样解决：
设置两个变量，maxpos 和 id 。maxpos 代表以snew[id]为中心的最长回文最右边界，即为maxpos=id+p[id]。
假设我们现在求p[i]，也就是以snew[i]为中心的最长回文半径，如果i < maxpos，如上图，那么p[i] = min(p[2 id - i], mx - i)
2 id - i其实就是等于 j ，p[j]表示以s_new[j]为中心的最长回文半径，见上图，因为 i 和 j 关于 id 对称，我们利用p[j]来加快查找。

复杂度分析

这样看起来很暴力，为什么复杂度是O(n)的呢？因为maxpos不会减小，每次暴力处理的时候，p[i]增大多少，就说明maxpos增大多少，而maxpos最多增加len次。所以复杂度是O(n)的。

代码

代码值得注意的是，p数组和snew数组务必要是字符串原串长度的两倍！不然会莫名TLE！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <iostream>
#include <string>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#define MAXN 110000 + 10
using namespace std;
char s[MAXN], snew[2 * MAXN];
int p[2 * MAXN];
inline int Init()
{
	int len = strlen(s);
	snew[0] = '$';		//防止在前面越界
	snew[1] = '#';
	int j = 2;
	for (register int i = 0; i < len; ++i)
	{
		snew[j++] = s[i];
		snew[j++] = '#';
	}
	snew[j] = '\0';		//防止在后面越界
	return j;
}
inline int Manacher()
{
	int maxlen = -1, len = Init();
	int id, maxpos = 0;
	for (register int i = 1; i < len; ++i)
	{
		if (i < maxpos) p[i] = min(p[id * 2 - i], maxpos - i);
		else p[i] = 1;
		while (snew[i - p[i]] == snew[i + p[i]]) p[i]++;
		if (maxpos < i + p[i])
			id = i, maxpos = i + p[i];
		maxlen = max(maxlen, p[i] - 1);
	}
	return maxlen;
}
int main(int argc, char **argv)
{
	ios::sync_with_stdio(false);
	while (cin >> s) cout << Manacher() << endl;
	return 0;
}
-------------本文结束了哦感谢您的阅读-------------